Lie Theory for the Roboticist
Why we need Lie theory?
作为全文的开始,在不引入其他概念的情况下简要回答一下这个问题。因为我们需要在机器人学中研究旋转与位姿估计,而这一切通常都是由齐次坐标下的矩阵运算完成的。但显然,我们很难研究矩阵的微小扰动和求导。以一个很常见的最小二乘法为例,考虑一个待估计的旋转矩阵$\mathbf{R}$和位姿真值$\mathbf{y}$:
\[\mathbf{\hat R} = \arg\min_R||\mathbf{y}-f(\mathbf{R})||^2\]通常情况下对于复杂的函数,我们一般是用迭代的方式进行求解,那么问题来了,对于迭代的方式求解最小二乘,我们无法利用梯度下降法找到一个$\Delta \mathbf{R}$使迭代进行下去,因为我们并没有对矩阵的导数定义。事实上,矩阵的增量是左乘而不是加。因此,一句话解答这个问题就是,我们需要李代数来把李群中的元素(例如旋转矩阵)映射到线性空间(旋转的向量表示)从而便于运算。
The following passage from Howe3 may serve us to illustrate what we leave behind:
Amazingly, the group $G$ is almost completely determined by $\mathfrak{g}$ and its Lie bracket. Thus for many purposes one can replace $G$ with $\mathfrak{g}$. Since $G$ is a complicated nonlinear object and $\mathfrak{g}$ is just a vector space, it is usually vastly simpler to work with $\mathfrak{g}$. This is one source of the power of Lie theory.”
What is a Lie Group?
设想我们有一个空间,这个空间中的每一个点都是$3\times3$ 矩阵。在这其中有一些特殊的矩阵能够满足一些性质,使得他们获得了一个特殊的名字:“旋转矩阵”。这些性质使得这些矩阵从一般的三维矩阵中凸显出来,我们把这些矩阵构成的集合记为$SO(3)$。 对于这些旋转矩阵,可以证明它们都满足以下的性质:具有正交性,且行列式的值为$1$1:
Rotation criterion: A rotation about $O$ in $\mathbb{R}^{3\times 3}$ is a linear transformation that preserves length and orientation. An $3\times 3$ real matrix $A$ represents a rotation of $\mathbb{R}^{3\times 3}$ if and only if $AA^T = 1$ and $\det(A) = 1$.
如同三维欧式空间中,到原点距离为$1$的点构成了一个单位球一样,这些行列式为$1$的三维正交矩阵也在这个矩阵空间构成了一个图形,我们无法把它很准确的可视化出来,不过不妨将它想象成一个特殊的球,球上的每一个点都代表了一个三维旋转矩阵。设想我们在三维空间从初始坐标轴开始旋转一个物体,这个物体的位姿在空间可以很自然的连续变化,而因此作用于这一物体的旋转变换也可以连续的在之前提到的“特殊的球”上移动。这个图形是联通的,($\det(A) = 1$是必须的,如果没有这个条件的话就不联通了)可以证明1:
Path connectedness of $SO(3)$: $SO(3)$ is path-connected, that is, if we view $3\times 3$ matrices as points of $\mathbb{R}^9$ in the natural way-by interpreting the $3\times 3$ matrices as the coordinates of a point, then any two points in $SO(3)$ may be connected by a continuous path.
说了这么多好像还没有和 Lie Group 扯上关系,不过不着急,刚才我们只是考虑了一个旋转矩阵,现在我们考虑两个旋转变换的复合。当我们对一个物体先作用$R_1$再做用$R_2$时,有$R = R_2R_1$。显然新的$R$也是一个旋转矩阵,当然它也在我们“特殊的球”上。事实上,刚才提到的作用于三维空间物体上的连续变换,也可以被当成很多个旋转变换的复合。而这些旋转变换依次复合得到的矩阵就构成了从初始坐标轴到最终的旋转$R$的路径。当我们在考虑两个旋转的复合时,很自然地给这些矩阵构成的集合$SO(3)$引入了矩阵乘法这样一个运算,这个运算实现了$SO(3)\times SO(3)\rightarrow SO(3)$。事实上,对于集合$SO(3)$和矩阵乘法这一运算,它们满足构成群的条件2,我们有:
$SO(3)$ is a finite dimensional smooth manifold $G$ together with a group structure on $G$, such that the multiplication $G\times G\rightarrow G$ and the attaching of an inverse $g\rightarrow g^{−1}: G\rightarrow G$ are smooth maps.
这里我们没有定义光滑流形,但直觉上讲,光滑流形就是一个连续的,不会尖锐突变的形状,这个条件保证了这样的流形可以实现求导。例如,Euclid 空间 $\mathbb{R}^n$是最简单的光滑流形。$SO(3)$作为一个群,同时又是一个光滑流形,我们称这样的群为李群。事实上,二维旋转矩阵,二维齐次变换矩阵,三维齐次变换矩阵都构成了李群。至此,我们回答了本节的题目,李群是一个具有群结构的光滑流形,群结构使我们可以在这个流行上进行计算,而光滑则保证了李群上可以定义微积分。
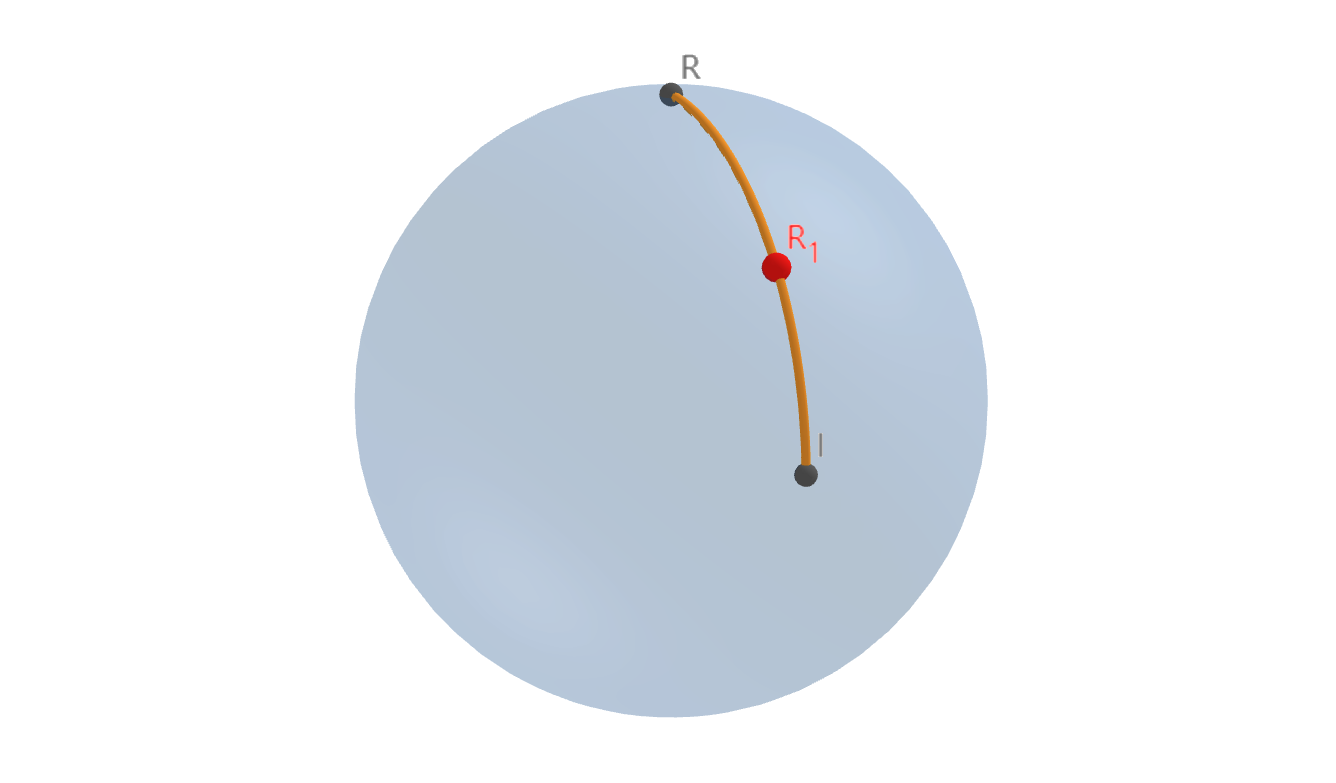
(注意上面这个图里,$R$,$R_1$和$I$代表的不是三维欧式空间单位球上的点,而是三维旋转矩阵,其中$I$是单位矩阵。对于任意一个旋转矩阵$R\in SO(3)$,从$I$可以找到一条经过$R_1$到达$R$的光滑路径)
From Lie group to Lie algebra
对于一个旋转变换而言,一般来说三个参数就足以表示。事实上,对于旋转矩阵表示,它的自由度为$9-6=3$;对于欧拉角表示,3个角度足以;对于单位四元数描述,它的自由度同样为$4-1=3$。这表明了每一个旋转矩阵都与一个三维向量一一对应,虽然目前我们还不知道这个对应关系如何寻找。旋转矩阵对应的三维向量正是$SO(3)$ Lie Group 对应的 Lie algebra,这一节我们来寻找它们之间的关系。
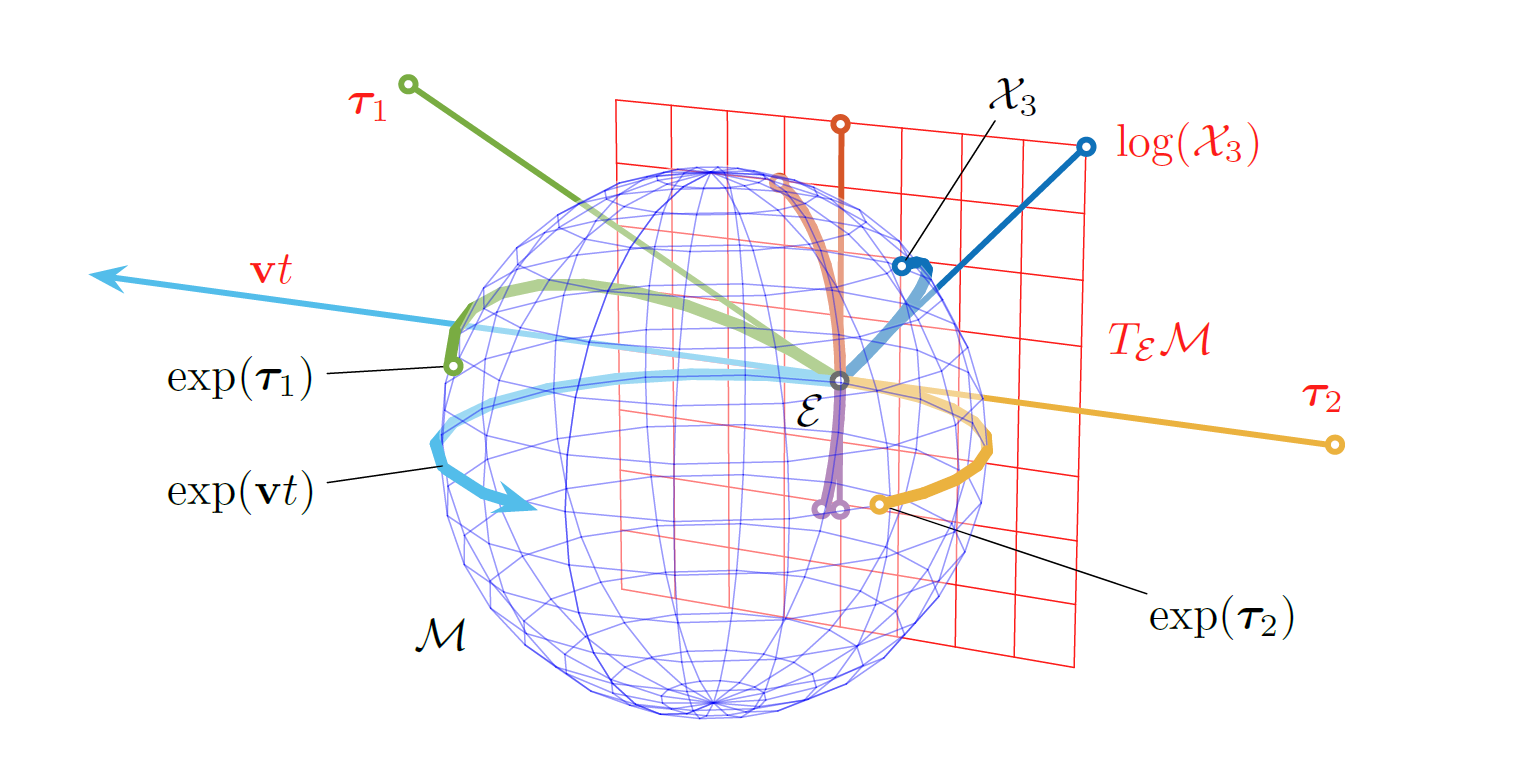
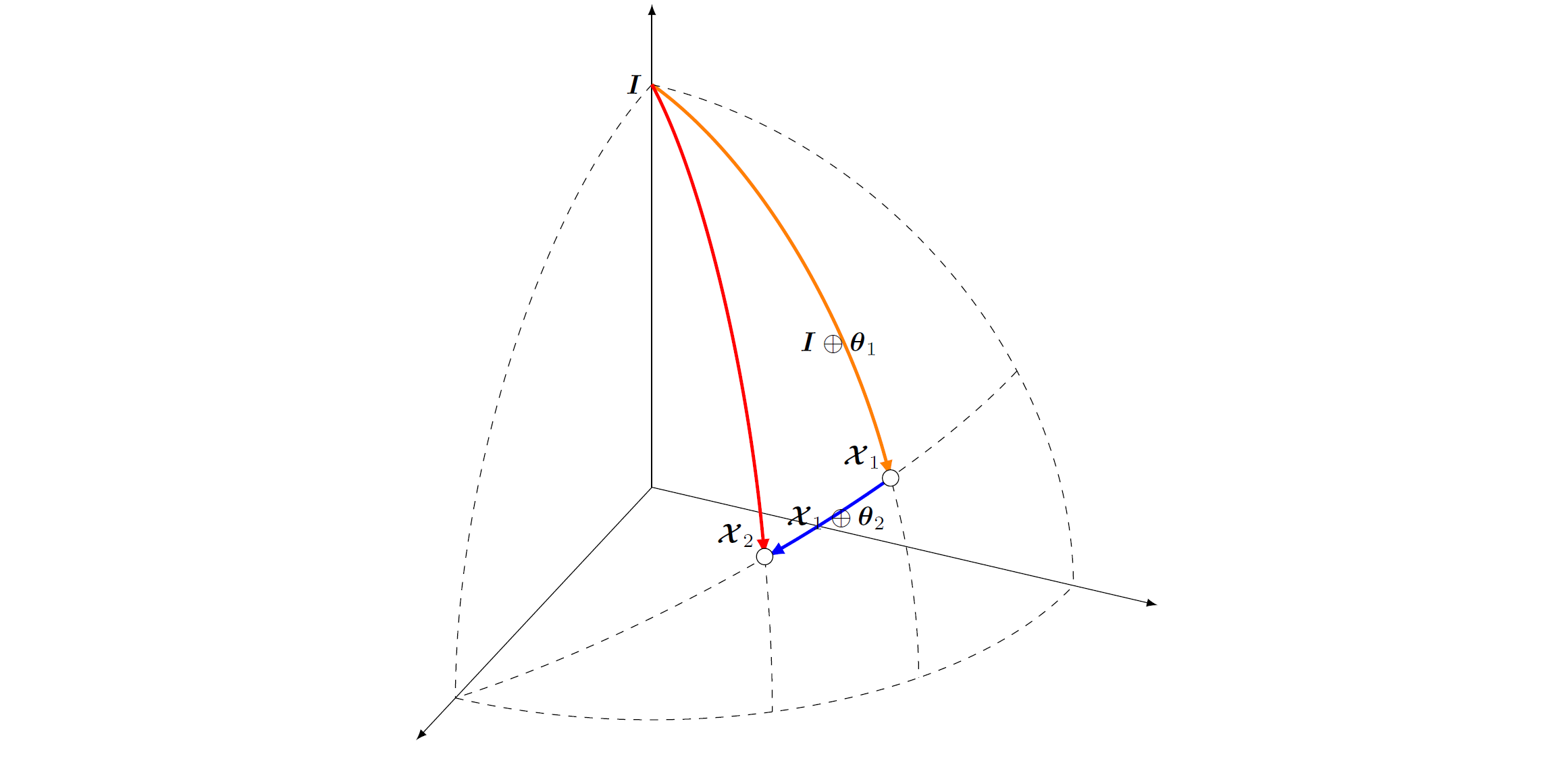
Summary
到这里,我们可以回答第一节的问题了,如何寻找一个合理的$\Delta \mathbf{R}$。考虑一个三维旋转$f: SO(3)\rightarrow \mathbb{R}^3$,$f(\textbf{R})=\textbf{Rp}$
Appendix
在这里,我们附加一个对$()^\wedge$运算符性质的证明:
对任意旋转矩阵$\mathbf{R}$ 和三维向量 $\mathbf{v}$,都有:$(\mathbf{Rv})^\wedge=\mathbf{Rv}^\wedge\mathbf{R}^T$
参考
- [1] Stillwell John, Naive lie theory, 2008
- [2] 東雲正樹, 知乎专栏:群论终极速成, 2022
- [3] Roger Howe, Very basic Lie theory, 1983