Reinforcement Learning Robotics Deep Learning

Legged Robot Articulation from Various References

Study the past if you would define the future.

Posted by Yubin on October 11, 2024

This is a summary of my presentation in my second Rinko at the University of Tokyo. In this Rinko, I chose the topic of Learning-Based Methods for Legged Robot Articulation from Various References.

Abstract

Legged robots have demonstrated remarkable potential in navigating complex and challenging environments, achieving significant progress and success in various applications over recent years. Recent advancements in robot hardware and reinforcement learning technologies have enabled these robots to exhibit agile locomotion within complex environments compared with traditional optimal control-based methods. This survey delves into the advancements in learning-based methods for robot articulation, highlighting their capability to train lifelike, agile robots that integrate prior knowledge from reference kinematic data while remaining environment-aware. Empirical studies showcase the maneuverability of quadruped robots across diverse terrains, reflecting their excellent performance and adaptability.

Introduction

Legged robots have shown significant potential to navigate complex and challenging environments, and we have witnessed explosive progress and substantial success in numerous applications over the past few years [1], [2]. The empirical demonstration of quadruped robots’ maneuverability across diverse terrains establishes their commendable performance. Various methodologies are utilized to enable quadruped, bipedal, and humanoid robots to navigate diverse terrains, with a notable focus in recent years on learning-based approaches [3][4][5][6][7][8]. The following figure shows examples of legged robots articulating in various environments.

Examples of notable learned behaviors for quadruped robots executed in the real world. [9]

To enable quadruped robots to perform agile maneuvers akin to their biological counterparts, such as dogs or cats, it is crucial to thoroughly explore and understand the robot’s action space. Inspired by curriculum learning, an incremental hardness training strategy is used to adapt the difficulty level for each terrain type individually [10]. With this curriculum learning strategy and sophisticated reward-engineering, robots can learn locomotion skills in challenging environments [4][7] or complete loco-manipulation tasks using their bodies and feet [11]. In such research, a teacher-student training framework is often utilized to transfer knowledge from the teacher to the student network. This training process can be considered a form of behavior cloning, where the robot learns to imitate the teacher’s motion.

However, the teacher’s motion can originate from various sources, such as motion capture data [12], videos [13], Model Predictive Control (MPC) planners [14], diffusion method-based motion generators [15], or even data generated by a Large Language Model (LLM) [16]. The following table illustrates the comparison of different reference motion sources. We list the advantages and disadvantages of each method in the table to highlight that each method has its own unique characteristics.

Comparison of different reference motion sources. Kinetic means whether the reference motion is kinetic data. Satisfies Robot's Morphology means the reference motion can be directly applied to robot without retargetting or mapping. Non-Craftwork refers to reference motions that are not being meticulously designed or hand-crafted directly or indirectly.

In this survey, we will investigate different methods for applying reference motions to robots and discuss their distinctions. In summary, we intend to introduce and discuss the following topics:

  • How to adapt the reference motion to the robot’s morphology and train the robot to imitate the motion.
  • How to learn a generalized motion prior that can be applied to various motions.
  • How to generate new actions based on the collected dataset, whether it is only kinematic data or not.
  • How to embed the text command into the robot’s motion reference using LLM.

We would like to first introduce some necessary backgrounds of learning-based articulation methods, including the Generative Adversarial Imitation Learning (GAIL) and generation model, which are the basic knowledge of following sections. Then the subsequent two sections will detail these topics. The final chapter will present the conclusion and outline avenues for future research.

Background

Generative Adversarial Imitation Learning

Imitation learning, also known as behavioral cloning, is used to train a policy to imitate an expert’s behavior, which may originally come from the automated driving area [17]. Given a dataset with observations and demonstrations, the policy is trained to minimize the difference between the output of the policy and the demonstration to imitate the expert.

However, imitation learning will suffer a drifting problem if only a small amount of demonstrations are available. Moreover, it is hard to derive the demonstrated action commands about motion data captured by real animals. To solve this problem, generative adversarial imitation learning (GAIL) [18] is utilized. GAIL is a method that combines imitation learning and generative adversarial networks (GANs) by learning a discriminator $D$ to measure the similarity between policy $\pi_\theta$ and expert trajectories $\tau_E \sim\pi_E$ using:

\[\mathcal{L}_{\text{GAIL}} = \mathbb{E}_{\tau_i}[\log(D_w(s,a))] + \mathbb{E}_{\tau_E}[\log(1-D_w(s,a))]\]

, where $w$ denotes the parameters of discriminator $D$. The policy is then trained using the reinforcement learning with rewards specified by:

\[r_t = \log(D_{w}(s_t,a_t))\]

Generally speaking, this reward function encourages the policy to generate actions that are not able to be distinguished from the demonstrations by the discriminator. The following algorithm shows the detailed training process of GAIL, which can be seen as a modern approach to imitation learning that builds on the foundational ideas of inverse reinforcement learning (IRL) but leverages adversarial training to directly learn policies.

Generative adversarial imitation learning (GAIL) [18]

Variational Auto-Encoder

Variational Auto-Encoders (VAEs) are a class of generative models that have gained substantial attention in the field of machine learning and artificial intelligence for their ability to learn latent representations of data and generate new data samples that are statistically similar to a given dataset. Introduced by Kingma and Welling in 2013, VAEs combine principles from Bayesian inference and neural networks, providing an elegant framework for unsupervised learning [19].

From a mathematical perspective, VAEs aim to maximize the Evidence Lower Bound (ELBO), which serves as a variational approximation to the true data likelihood. Mathematically, the ELBO for a VAE can be expressed as follows:

\[\mathcal{L}_{\text{VAE}}(\theta, \phi; \textbf{x}) = \mathbb{E}_{q_\phi(\textbf{z}|\textbf{x})} [\log p_\theta(\textbf{x}|\textbf{z})] - \text{KL}(q_\phi(\textbf{z}|\textbf{x}) || p(\textbf{z}))\]

, where $q_\phi(\textbf{z}|\textbf{x})$ represents the encoder network approximating the posterior distribution of latent variables given the data, $p_\theta(\textbf{x}|\textbf{z})$ represents the decoder network probabilistically reconstructing the data, and $p(\textbf{z})$ is the prior distribution over the latent variables.

Based on VAE architecture, researchers proposed Vector Quantized Variational Auto-Encoder (VQ-VAE) [20] in order to address some limitations of traditional VAE related to their latent space representations. At a high level, VQ-VAE modifies the standard VAE architecture by incorporating a vector quantization layer, which forces the encoder to output discrete latent codes rather than continuous ones to capture the underlying structure of the input data more effectively.

In VQ-VAE, the encoder maps the input to one latent embedding and the decoder maps the embedding back into an output to recover the input. The VQ-VAE training loss consists of a reconstruction loss and a commitment loss as denoted below:

\[\mathcal{L}_{\text{VQ-VAE}}(\theta, \phi; \textbf{x}) =\mathbb{E}_{q_\phi(\textbf{z}|\textbf{x})} [\log p_\theta(\textbf{x}|\textbf{z})] + \left\|sg\left[z^e(\textbf{x})\right]-\textbf{e}\right\|_2^2 + \beta\left\|z^e(\textbf{x})-{sg}[\textbf{e}]\right\|_2^2\]

, where the reconstruction loss for the input data $x$ is

\[\mathbb{E}_{q_\phi(\textbf{z}|\textbf{x})}[\log p_\theta(\textbf{x}|\textbf{z})]\]

; $sg$ is an operator to stop the gradients; $z^e(\textbf{x})$ is the output of the encoder; $\textbf{e}$ is the nearest embedding from the discrete latent embeddings to $z^e(x)$; and the hyperparameter $\beta$ balances the last two terms.

Diffusion Model and Applications

Introduced by Ho et al. in 2020, the diffusion model leverages the principles of Langevin dynamics to model the data distribution and generate new samples that are statistically similar to the original dataset [21]. From the perspective of VAE’s extension, the diffusion models are incremental updates where the assembly of the whole gives us the encoder-decoder structure [22]. We will not dive into the mathematical derivation of the diffusion model in this survey. The loss function during training is defined as:

\[\mathcal{L}_{\text{DM}}(\theta, t; \textbf{x}) = \mathbb{E}_{t, \textbf{x},\epsilon}[||\epsilon_t - \epsilon_{\theta}(\textbf{x}_t, t)||_2^2]\]

to minimize the difference between the predicted noise and the added noise, where $\epsilon_t$ is the noise added to the input data at time $t$, and $\epsilon_{\theta}(\textbf{x}_t, t)$ is the noise predicted by the model. And during sampling time, the model recovers images from standard Gaussian noise in $T$ time steps by:

\[\textbf{x}_{t-1} = \frac{1}{\sqrt{\alpha_t}}(\textbf{x}_t - \frac{1-\alpha_t}{\sqrt{1-\overline{\alpha}_t}}\epsilon_\theta(\textbf{x}_t, t)) + \sigma_t\textbf{z}\]

, where the $\alpha_t$ and $\overline{\alpha}_t$ are the parameters to control the diffusion process, $\sigma_t$ is a variance constant, and $\textbf{z}$ is a standard Gaussian noise.

The diffusion model has been applied to various fields, such as image generation [21], motion generation [23], and even robot control [24]. In motion diffusion model (MDM) [23], the model is fed a motion sequence $\textbf{x}^{1:N}_t$ of length N in a noising step t, as well as $t$ itself and a CLIP [25] based textual embedding $c$. In each sampling step, the transformer encoder predicts the final clean motion $\hat{\textbf{x}}_t^{1:N}$. The model is trained using the loss function before with an additional geometric loss term for regularization.

Learning from captured data

Adapt MoCap data to robot

Several types of research have been proposed to imitate reference motions in physics-based animation generation [26][27][28] However, due to the gap between simulation and the real world, it is hard to directly apply these methods to real robots. Some researchers use optimal control methods to retarget the mocap data or videos with noise due to the unpredictability of creature behavior to robot [29][30][13]. With recent advancements in reinforcement learning, in [12], the authors propose a method to adapt the reference motion to the robot with three stages: motion retargeting, motion imitation, and domain adaptation.

Motion Retargeting: In motion retargeting, the source motions are retargeted to the robot’s morphology using inverse kinematics (IK). A set of source key points from the subject’s body are paired with corresponding on the robot, which is illustrated in the following figure. With the robot’s pose $\textbf{q}_t$ and the IK solver $\textbf{x}_i(\textbf{q}_t)$ for each point $i$, the source motion can be retargeted to the robot’s morphology by:

\[\arg\min_{\textbf{q}_{0:T}} \sum_t\sum_i ||\hat{\textbf{x}}_i(t)-\textbf{x}_i(\textbf{q}_t)||^2 + (\bar{\textbf{q}} - \textbf{q}_t)^T\textbf{W}(\bar{\textbf{q}} - \textbf{q}_t)\]

, where $T$ is the time sequence length, and $\textbf{W}$ denotes a diagonal matrix with weights for each joint to let the robot remain similar to the default pose $\bar{\textbf{q}}$ as a regularization term.

Motion Imitation: During motion imitation, the robot is trained to imitate the retargeted motion in a reinforcement learning approach. The policy $\pi_\theta$ is trained to minimize the difference between the output of the policy and the retargeted motion using reward $r_t$: $r_t = \sum_iw^ir_t^i$ , where $i$ denotes different kinds of rewards designed by the author to encourage the robot to minimize the tracking errors on both root and joint positions and velocities and $w^i$ is the weight for each reward. The following table shows the detailed reward design, which is similar to the same tasks in computer graphics named DeepMimic [31].

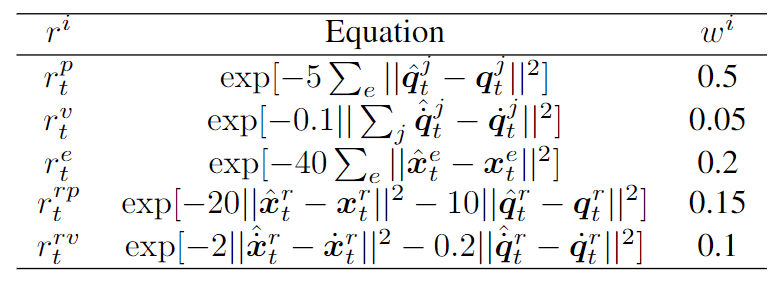
Reward function elements for sequence tracking in [12]. The rewards are designed to encourage the robot to minimize the tracking errors on joint pose $\textbf{q}_t^{j}$, joint velocity $\dot{\textbf{q}}_t^{j}$, end-effector pose $\textbf{x}_t^{e}$, root pose $\textbf{x}_t^{r}$, and root velocity $\dot{\textbf{x}}_t^{r}$, respectively.

Domain Adaptation: Furthermore, to reduce the gap between simulation and the real world, the authors propose a domain adaptation method to encode the physical parameters $\mu$ with domain randomization $\mu \sim p(\mu)$. To prevent the encoder from overfitting and encourage the policy to be robust to physical uncertainty, they add the term as an information bottleneck like introduced in [32] to the reward function as:

\[\arg\max_{\pi_\theta, E} \mathbb{E}_{\mu \sim p(\mu)} \mathbb{E}_{\textbf{z} \sim E(\textbf{z}|\mu)} \mathbb{E}_{\tau\sim p(\tau|\pi,\mu,\textbf{z})} [\sum_{t=0}^{T-1}\gamma^tr_t] -\beta \mathbb{E}_{\mu \sim p(\mu)}[D_{KL}[E(\cdot|\mu)||\rho(\cdot)]]\]

, where $E(\textbf{z}|\mu)$ is the physical parameter encoder, $\textbf{z}$ is the encoded physical parameters, $\rho(\cdot)$ is a variational prior for $\textbf{z}$, and $\tau\sim p(\tau|\pi,\mu,\textbf{z})$ are trajectories sampled from the policy $\pi_\theta$ with physical parameters $\mu$ and encoded vector $\textbf{z}$. Here $\beta$ can be treated as a Lagrangian multiplier to balance the information bottleneck and reward.

With the domain adaptation method, the robot shows a better performance in new environments especially for dynamic skills. The following figure shows the robot performing dog backward trotting learned by imitating backward played reference motions. Comparison results show that the adaptive policies outperform their non-adaptive counterparts in most skills.

Comparison result. Top: Corresponding keypoints (red points) between dog skeleton (Left) and quadruped robot (Right). Bottom: Laikago robot performing dog backward trotting learned by imitating reference motions [12].

References

  1. Hendra H, Liu Y, Ishikawa R, Oishi T, Sato Y: Quadruped Robot Platform for Selective Pesticide Spraying. In 2023 18th International Conference on Machine Vision and Applications (MVA). . IEEE; 2023:1–6.

  2. DeFazio D, Hirota E, Zhang S: Seeing-Eye Quadruped Navigation with Force Responsive Locomotion Control. In Conference on Robot Learning. . PMLR; 2023:2184–2194.

  3. Kumar A, Fu Z, Pathak D, Malik J: Rma: Rapid motor adaptation for legged robots. arXiv preprint arXiv:210704034 2021,

  4. Zhuang Z, Fu Z, Wang J, Atkeson CG, Schwertfeger S, Finn C, Zhao H: Robot Parkour Learning. In Conference on Robot Learning. . PMLR; 2023:73–92.

  5. Haarnoja T, Moran B, Lever G, Huang SH, Tirumala D, Humplik J, Wulfmeier M, Tunyasuvunakool S, Siegel NY, Hafner R, et al.: Learning agile soccer skills for a bipedal robot with deep reinforcement learning. Science Robotics 2024, 9:eadi8022.

  6. Agarwal A, Kumar A, Malik J, Pathak D: Legged locomotion in challenging terrains using egocentric vision. In Conference on robot learning. . PMLR; 2023:403–415.

  7. Cheng X, Shi K, Agarwal A, Pathak D: Extreme parkour with legged robots. In 2024 IEEE International Conference on Robotics and Automation (ICRA). . IEEE; 2024:11443–11450.

  8. Duan H, Pandit B, Gadde MS, Van Marum B, Dao J, Kim C, Fern A: Learning vision-based bipedal locomotion for challenging terrain. In 2024 IEEE International Conference on Robotics and Automation (ICRA). . IEEE; 2024:56–62.

  9. Ha S, Lee J, Panne M van de, Xie Z, Yu W, Khadiv M: Learning-based legged locomotion; state of the art and future perspectives. arXiv preprint arXiv:240601152 2024,

  10. Rudin N, Hoeller D, Reist P, Hutter M: Learning to walk in minutes using massively parallel deep reinforcement learning. In Conference on Robot Learning. . PMLR; 2022:91–100.

  11. Cheng X, Kumar A, Pathak D: Legs as manipulator: Pushing quadrupedal agility beyond locomotion. In 2023 IEEE International Conference on Robotics and Automation (ICRA). . IEEE; 2023:5106–5112.

  12. Peng XB, Coumans E, Zhang T, Lee T-W, Tan J, Levine S: Learning agile robotic locomotion skills by imitating animals. arXiv preprint arXiv:200400784 2020,

  13. Zhang JZ, Yang S, Yang G, Bishop AL, Gurumurthy S, Ramanan D, Manchester Z: Slomo: A general system for legged robot motion imitation from casual videos. IEEE Robotics and Automation Letters 2023,

  14. Jenelten F, He J, Farshidian F, Hutter M: Dtc: Deep tracking control. Science Robotics 2024, 9:eadh5401.

  15. Agon S, Ruben G, Espen K, Markus G, Moritz B: Robot Motion Diffusion Model: Motion Generation for Robotic Characters. In ACM SIGGRAPH Asia. . 2024.

  16. Tang Y, Yu W, Tan J, Zen H, Faust A, Harada T: Saytap: Language to quadrupedal locomotion. arXiv preprint arXiv:230607580 2023,

  17. Bojarski M, Del Testa D, Dworakowski D, Firner B, Flepp B, Goyal P, Jackel LD, Monfort M, Muller U, Zhang J, et al.: End to end learning for self-driving cars. arXiv preprint arXiv:160407316 2016,

  18. Ho J, Ermon S: Generative adversarial imitation learning. In Proceedings of the 30th International Conference on Neural Information Processing Systems. . 2016:4572–4580.

  19. Kingma DP: Auto-encoding variational bayes. arXiv preprint arXiv:13126114 2013,

  20. Van Den Oord A, Vinyals O, others: Neural discrete representation learning. Advances in neural information processing systems 2017, 30.

  21. Ho J, Jain A, Abbeel P: Denoising diffusion probabilistic models. Advances in neural information processing systems 2020, 33:6840–6851.

  22. Chan SH: Tutorial on Diffusion Models for Imaging and Vision. arXiv preprint arXiv:240318103 2024,

  23. Tevet G, Raab S, Gordon B, Shafir Y, Cohen-or D, Bermano AH: Human Motion Diffusion Model. In The Eleventh International Conference on Learning Representations . . 2023.

  24. Chi C, Feng S, Du Y, Xu Z, Cousineau E, Burchfiel B, Song S: Diffusion policy: Visuomotor policy learning via action diffusion. arXiv preprint arXiv:230304137 2023,

  25. Radford A, Kim JW, Hallacy C, Ramesh A, Goh G, Agarwal S, Sastry G, Askell A, Mishkin P, Clark J, et al.: Learning transferable visual models from natural language supervision. In International conference on machine learning. . PMLR; 2021:8748–8763.

  26. Zhang H, Starke S, Komura T, Saito J: Mode-adaptive neural networks for quadruped motion control. ACM Transactions on Graphics (TOG) 2018, 37:1–11.

  27. Liu L, Hodgins J: Learning to schedule control fragments for physics-based characters using deep q-learning. ACM Transactions on Graphics (TOG) 2017, 36:1–14.

  28. Yao H, Song Z, Chen B, Liu L: ControlVAE: Model-Based Learning of Generative Controllers for Physics-Based Characters. ACM Transactions on Graphics (TOG) 2022, 41:1–16.

  29. Kang D, Zimmermann S, Coros S: Animal gaits on quadrupedal robots using motion matching and model-based control. In 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). . IEEE; 2021:8500–8507.

  30. Grandia R, Farshidian F, Knoop E, Schumacher C, Hutter M, Bächer M: Doc: Differentiable optimal control for retargeting motions onto legged robots. ACM Transactions on Graphics (TOG) 2023, 42:1–14.

  31. Peng XB, Abbeel P, Levine S, Panne M Van de: Deepmimic: Example-guided deep reinforcement learning of physics-based character skills. ACM Transactions On Graphics (TOG) 2018, 37:1–14.

  32. Alemi AA, Fischer I, Dillon JV, Murphy K: Deep variational information bottleneck. arXiv preprint arXiv:161200410 2016,

CATALOG
    FEATURED TAGS
    Computer Vision Deep Learning
    FRIENDS